(पेपर) एस.एस.सी सीजीएल (टीयर -2) परीक्षा - 2017 "20 फरवरी 2018 को आयोजित" सुबह पाली "(मात्रात्मक क्षमता)
(पेपर) एस.एस.सी सीजीएल (टीयर -2) परीक्षा - 2017 "20 फरवरी 2018 को आयोजित" सुबह पाली "(मात्रात्मक क्षमता)
QID : 1 - निम्नलिखित में से कौन सा/से कथन सत्य है/हैं?
I. 333 > 333
II. 333 > (33)3
Options:
1) केवल I
2) केवल II
3) I तथा II दोनों
4) न तो I न ही II
Correct Answer: न तो I न ही II
QID : 2 - यदि P = 22 + 62 + 102 + 142 + … 942 तथा Q = 12 + 52 + 92 + … 812 हैं, तो P – Q का मान क्या है?
Options:
1) 24645
2) 26075
3) 29317
4) 31515
Correct Answer: 26075
QID : 3 - यदि A = (1/0.4) + (1/0.04) + (1/0.004) + … 8 पदों तक हैं, तो A का मान क्या है?
Options:
1) 27272727.5
2) 25252525.5
3) 27777777.5
4) 25555555.5
Correct Answer: 27777777.5
QID : 4 - यदि M = 0.1 + (0.1)2 + (0.01)2 तथा N = 0.3 + (0.03)2 + (0.003)2 हैं, तो M + N का मान क्या है?
Options:
1) 0.411009
2) 0.413131
3) 0.313131
4) 0.131313
Correct Answer: 0.411009
QID : 5 -

Options:
1) P < Q < R
2) R < Q < P
3) Q < P < R
4) R < P < Q
Correct Answer: R < Q < P
QID : 6 -

Options:
1) केवल I
2) केवल II
3) केवल III
4) कोई सत्य नहीं है।
Correct Answer: केवल I
QID : 7 -

Options:
1) केवल I
2) केवल II
3) I तथा II दोनों
4) न तो I न ही II
Correct Answer: केवल I
QID : 8 - निम्नलिखित में से कौन सा/से कथन सत्य है/हैं?
I. 72 के कुल 12 धनात्मक गुणनखण्ड हैं।
II. प्रथम 20 विषम संख्याओं का योग 400 है।
III. दो अंकों की सबसे बड़ी अभाज्य संख्या 97 है।
Options:
1) केवल I तथा II
2) केवल II तथा III
3) केवल I तथा III
4) सभी सत्य हैं।
Correct Answer: सभी सत्य हैं।
QID : 9 - यदि M = (3/7) ÷ (6/5) × (2/3) + (1/5) × (3/2) तथा N = (2/5) × (5/6) ÷ (1/3) + (3/5) × (2/3) ÷ (3/5) हैं, तो M/N का मान क्या है?
Options:
1) 207/560
2) 339/1120
3) 113/350
4) 69/175
Correct Answer: 113/350
QID : 10 - M, 4 अंकों की सबसे बड़ी संख्या है, जिसे 4, 5, 6 तथा 7 से विभाजित करने पर शेषफल क्रमशः 2, 3, 4 तथा 5 आता हैं। जब M को 9 से विभाजित किया जाये, तो शेषफल क्या होगा?
Options:
1) 2
2) 1
3) 3
4) 6
Correct Answer: 1
पेपर डाउनलोड करने के लिए यहां क्लिक करें
एसएससी - कर्मचारी चयन आयोग (सीजीएल) परीक्षा अध्ययन सामग्री
एसएससी CGL (टीयर -1) परीक्षा के लिए ऑनलाइन कोचिंग
Study Kit for SSC CGL (Tier-2) Exam
SSC CGL Tier-1 EXAM Printed Study Kit
QID : 11 - निम्नलिखित में से कौन सा/से कथन सत्य है/हैं?
I. √11 + √7 < √10 + √8.
II. √17 + √11 > √15 + √13
Options:
1) केवल I
2) केवल II
3) I तथा II दोनों
4) न तो I न ही II
Correct Answer: केवल I
QID : 12 -

Options:
1) केवल I तथा II
2) केवल I तथा III
3) केवल I
4) सभी सत्य हैं।
Correct Answer: केवल I तथा II
QID : 13 - यदि x + y + z = 22 तथा xy + yz + zx = 35 हैं, तो (x – y)2 + (y – z)2 + (z – x)2 का मान क्या है?
Options:
1) 793
2) 681
3) 758
4) 715
Correct Answer: 758
QID : यदि (x + y)/z = 2 है, तो [y/(y – z)] + [x/(x – z)] का मान क्या है?
Options:
1) 0
2) 1
3) 2
4) – 1
Correct Answer: 2
QID : 15 - यदि α तथा β समीकरण x2 – 2x + 4 = 0,के मूल हैं, तो वह समीकरण क्या है जिसके मूल α3/β2 and β3/α2 हैं?
Options:
1) x2 – 4 x + 8 = 0
2) x2 – 32 x + 4 = 0
3) x2 – 2 x + 4 = 0
4) x2 – 16 x + 4 = 0
Correct Answer: x2 – 2 x + 4 = 0
QID : 16 - यदि समीकरण Ax2 +Bx + C = 0 का एक मूल दूसरे से ढाई गुणा है, तो निम्नलिखित में से कौन सा सत्य है?
Options:
1) 7B2 = 3 CA
2) 7B2 = 4 CA
3) 7B2 = 36 CA
4) 10B2 = 49 CA
Correct Answer: 10B2 = 49 CA
QID : 17 - यदि x2 – 12x + 33 = 0 है, तो (x – 4)2 + [1/(x – 4)2] का मान क्या है?
Options:
1) 16
2) 14
3) 18
4) 20
Correct Answer: 14
QID : 18 - यदि a4 + 1 = [a2/b2] (4b2 – b4 – 1) है, तो a4 + b4 का मान क्या है?
Options:
1) 2
2) 16
3) 32
4) 64
Correct Answer: 2
QID : 19 -
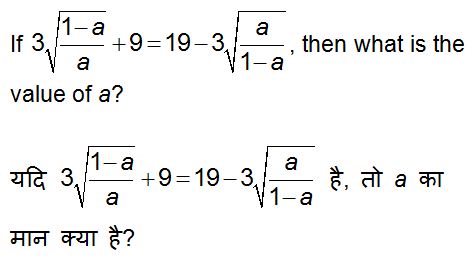
Options:
1) 3/10, 7/10
2) 1/10, 9/10
3) 2/5, 3/5
4) 1/5, 4/5
Correct Answer: 1/10, 9/10
QID : 20 -
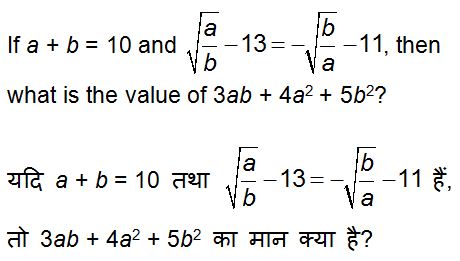
Options:
1) 450
2) 300
3) 600
4) 750
Correct Answer: 300
QID : 21 - यदि 3x + 4y – 2z + 9 = 17, 7x + 2y + 11z + 8 = 23 तथा 5x + 9y + 6z – 4 = 18 हैं, तो x + y + z – 34 का मान क्या है?
Options:
1) – 28
2) – 14
3) – 31
4) – 45
Correct Answer: – 31
QID : 22 -
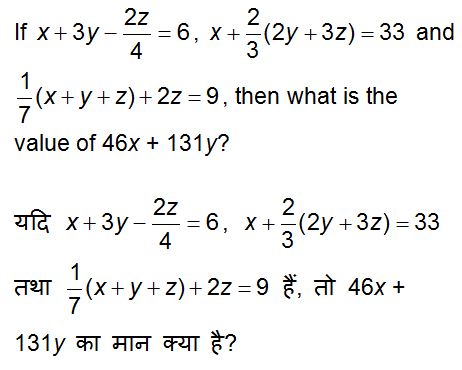
Options:
1) 414
2) 364
3) 384
4) 464
Correct Answer: 414
QID : 23 -

Options:
1) 1 : 1
2) 1 : 4
3) 2 : 3
4) 5 : 2
Correct Answer: [ No Correct Answer ]
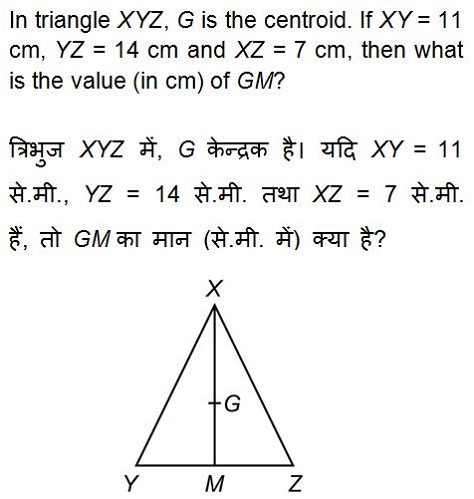
QID : 24 -
Options:
1) 6
2) 4
3) 2
4) 3
Correct Answer: 2
QID : 25 -
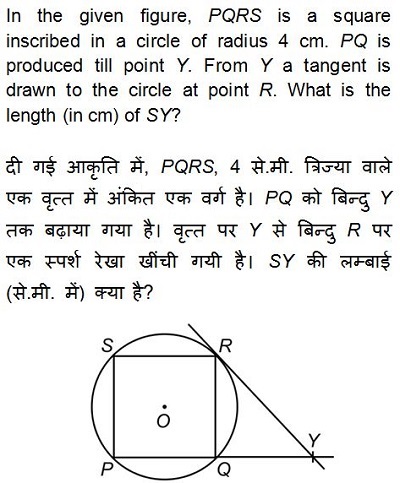
Options:
1) 4√10
2) 2√10
3) 6√10
4) 3√5
Correct Answer: 4√10
QID : 26 - एक समलम्ब में, एक विकर्ण दूसरे विकर्ण को 2 : 9 के अनुपात में विभाजित करता है। यदि दो समांतर भुजाओं में से सबसे बड़ी भुजा की लम्बाई 45 से.मी. है, तो दूसरी समांतर भुजा की लम्बाई (से.मी. में) क्या है?
Options:
1) 10
2) 5
3) 18
4) 14
Correct Answer: 10
QID : 27 -

Options:
1) [(5√3) – 3]
2) [(4√3) – 2]
3) [(2√5) – 1]
4) [(2√6) – 1]
Correct Answer: [(2√6) – 1]
QID : 28 -

Options:
1) 5√10
2) 4√10
3) 8√5
4) 16√2
Correct Answer: 5√10
QID : 29 -
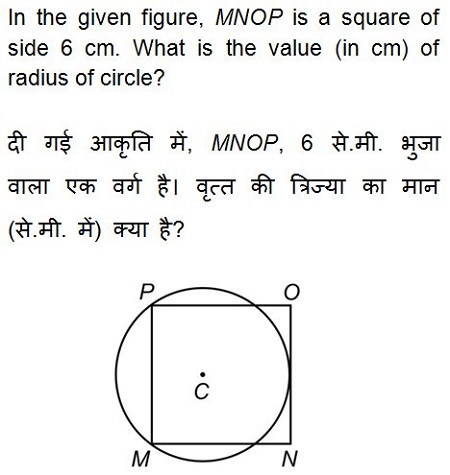
Options:
1) 4.25
2) 3.75
3) 3.5
4) 4.55
Correct Answer: 3.75
QID : 30 -
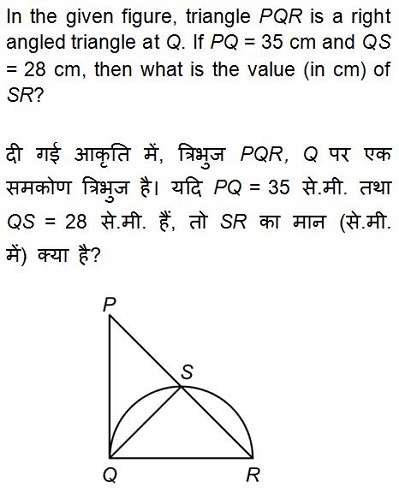
Options:
1) 35.33
2) 37.33
3) 41.33
4) 43.33
Correct Answer: 37.33
QID : 31 -

Options:
1) 1 : 4
2) 2 : 5
3) 1 : 3
4) 2 : 7
Correct Answer: 1 : 3
QID : 32 - दो वृत्तों के केन्द्रों के मध्य की दूरी 61 से.मी. है तथा उनकी त्रिज्याएँ 35 से.मी. तथा 24 से.मी. हैं। वृत्तों की उभयनिष्ठ अनुस्पर्श रेखा की लम्बाई (से.मी. में) क्या है?
Options:
1) 60
2) 54
3) 48
4) 72
Correct Answer: 60
QID : 33 -
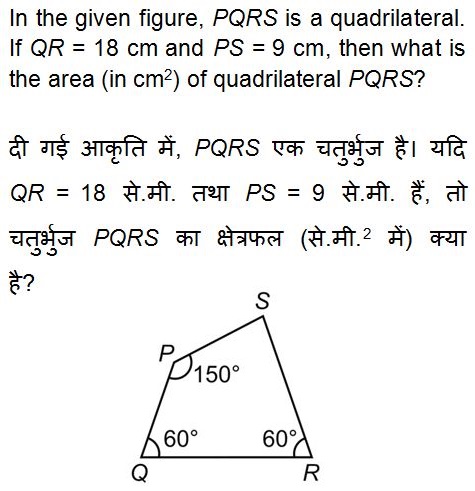
Options:
1) (64√3)/3
2) (177√3)/2
3) (135√3)/2
4) (98√3)/3
Correct Answer: (135√3)/2
QID : 34 - PQR एक त्रिभुज है, जिसका क्षेत्रफल 180 से.मी.2 है। S, भुजा QR पर एक बिन्दु इस प्रकार है कि PS, ∠QPR पर कोण द्विभाजक है। यदि PQ : PR = 2 : 3 है, तो त्रिभुज PSR का क्षेत्रफल (से.मी.2 में) क्या है?
Options:
1) 90
2) 108
3) 144
4) 72
Correct Answer: 108
QID : 35 -

Options:
1) 98
2) 196
3) 122.5
4) 171.5
Correct Answer: 196
QID : 36 - ABCDEF 12 से.मी. भुजा वाला एक सम षट्भुज है। त्रिभुज ECD का क्षेत्रफल (से.मी.2 में) क्या है?
Options:
1) 18√3
2) 24√3
3) 36√3
4) 42√3
Correct Answer: 36√3
QID : 37 - PQRS, 16 से.मी. भुजा वाला एक वर्ग है। दिये गये वर्ग से काटे जा सकने वाले सबसे बड़े सम अष्ट्भुज की भुजा का मान (से.मी. में) क्या है?
Options:
1) 8 – 4√2
2) 16 + 8√2
3) 16√2 – √16
4) 16 – 8√2
Correct Answer: 16√2 – √16
QID : 38 -
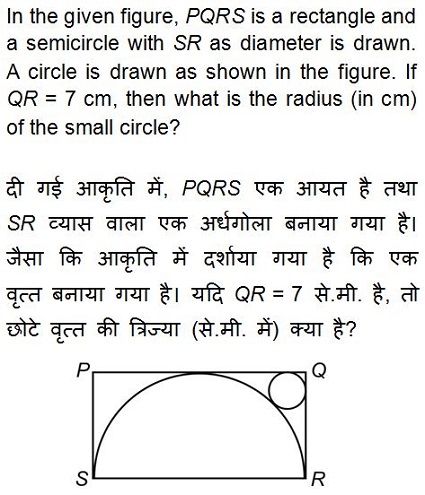
Options:
1) 21 + 14√2
2) 21 – 14√2
3) 21 + 14√2 तथा 21 – 14√2 दोनों
4) इनमें से कोई नहीं
Correct Answer: 21 – 14√2
QID : 39 -
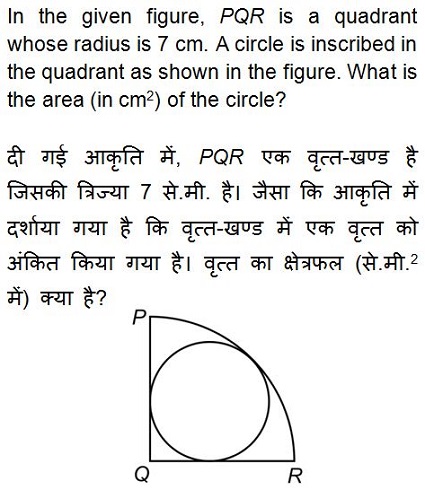
Options:
1) 385 – 221√2
2) 308 – 154√2
3) 154 – 77√2
4) 462 – 308√2
Correct Answer: 462 – 308√2
QID : 40 - एक प्रिज़्म का आधार, एक 6 से.मी. भुजा वाला समषट्भुज है। यदि प्रिज़्म का कुल पृष्ठीय क्षेत्रफल 216√3 से.मी.2 है, तो प्रिज़्म की लम्बाई (से.मी. में) क्या है?
Options:
1) 3√3
2) 6√3
3) 6
4) 3
Correct Answer: 3√3
QID : 41 - एक ठोस शंकु के आधार की त्रिज्या 9 से.मी. है तथा उसकी ऊँचाई 21 से.मी. है। इसे दो कटाव, जो आधार के समांतर है से 3 भागों में काटा गया। कटाव आधार से क्रमशः 7 से.मी. तथा 14 से.मी. की ऊँचाई पर हैं। क्रमशः ऊपरी, मध्य तथा निचले भागों के वक्र पृष्ठीय क्षेत्रफल का अनुपात क्या है?
Options:
1) 1 : 4 : 8
2) 1 : 3 : 5
3) 1 : 3 : 9
4) 1 : 6 : 12
Correct Answer: 1 : 3 : 5
QID : 42 -एक लम्बवत गोलाकार बेलन की लम्बाई 18 से.मी. तथा त्रिज्या 7 से.मी. है। बेलन को तीन बराबर भागों में काटा जाता हैं (आधार के समांतर 2 कटाव द्वारा)। कुल पृष्ठीय क्षेत्रफल में कितने प्रतिशत की वृद्धि हुई है?
Options:
1) 62
2) 56
3) 48
4) 52
Correct Answer: 56
QID : 43 - एक बेलन के वक्र पृष्ठीय क्षेत्रफल तथा आयतन का अनुपात 1 : 7 है। कुल पृष्ठीय क्षेत्रफल तथा आयतन का अनुपात 187 : 770 है। इसके आधार की त्रिज्या तथा ऊँचाई क्रमशः अनुपात क्या है?
Options:
1) 5 : 8
2) 4 : 9
3) 3 : 7
4) 7 : 10
Correct Answer: 7 : 10
QID : 44 - एक गोले के कुल पृष्ठीय क्षेत्रफल तथा आयतन का अनुपात 1 : 7 है। इस गोले को पिघलाकर बराबर माप के छोटे गोले बनाये जाते हैं। प्रत्येक छोटे गोले की त्रिज्या बड़े गोले की त्रिज्या की 1/6 हैं। सभी छोटे गोलों के वक्र पृष्ठीय क्षेत्रफल का योग (से.मी.2 में) क्या है?
Options:
1) 31276
2) 36194
3) 25182
4) 33264
Correct Answer: 33264
QID : 45 -

Options:
1) 3318.33
2) 3462.67
3) 3154.67
4) 3248.33
Correct Answer: 3462.67
QID : 46 - एक ठोस घन की भुजा 8 से.मी. है। वह ऊपर सतह के विकर्णों पर 4 समान भागों में काटा जाता हैं। प्रत्येक भाग का कुल पृष्ठीय क्षेत्रफल (से.मी.2 में) क्या है?
Options:
1) 96 + 64√2
2) 80 + 64√2
3) 96 + 48√2
4) 80 + 48√2
Correct Answer: 96 + 64√2
QID : 47 - एक सम पिरामिड का आधार एक वर्ग है। पिरामिड की ऊँचाई 22 से.मी. है तथा उसके आधार की भुजा 14 से.मी. है। पिरामिड का आयतन एक गोले के आयतन के बराबर है। गोले की त्रिज्या (से.मी. में) क्या है?
Options:
1)
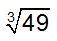
2) 7
3) 14
4)
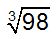
Correct Answer: 7
QID : 48 - [sin (y – z) + sin (y + z) + 2 sin y]/[sin (x – z) + sin (x + z) + 2 sin x] का मान क्या है?
Options:
1) cos x sin y
2) (sin y)/(sin x)
3) sin z
4) sin x tan y
Correct Answer: (sin y)/(sin x)
QID : 49 - {[sin (x + y) – 2 sin x + sin (x – y)]/[cos (x – y) + cos (x + y) – 2 cos x]} × [(sin 10x – sin 8x)/(cos 10x + cos 8x)] का मान क्या है?
Options:
1) 0
2) tan2 x
3) 1
4) 2 tan x
Correct Answer: tan2 x
QID : 50 - [sin (90o – 10θ) – cos (p – 6θ)]/ [cos (p/2 – 10θ) – sin (p – 6θ)] का मान क्या है?
Options:
1) tan 2θ
2) cot 2θ
3) cot θ
4) cot 3θ
Correct Answer: cot 2θ
QID : 51 - यदि sec θ (cos θ + sin θ) = √2 है, तो (2 sin θ)/(cos θ – sin θ) का मान क्या है?
Options:
1) 3√2
2) 3/√2
3) 1/√2
4) √2
Correct Answer: √2
QID : 52 -

Options:
1) tan2 θ sec2 θ
2) sec4 θ
3) tan4 θ
4) tan2 θ sin2 θ
Correct Answer: tan2 θ sec2 θ
QID : 53 - [tan (90 – A) + cot (90 – A)]2/[2 sec2 (90 – 2A)] का मान क्या है?
Options:
1) 0
2) 1
3) 2
4) – 1
Correct Answer: 2
QID : 54 - {sin (90 – x) cos [π – (x – y)]} + {cos (90 – x) sin [π – (y – x)]} का मान क्या है?
Options:
1) -cos y
2) -sin y
3) cos x
4) tan y
Correct Answer: -cos y
QID : 55 - मैदान पर एक बिन्दु से एक हवाई जहाज़ का उन्नयन कोण 60o है। 30 सेकण्ड उड़ने के पश्चात, उन्नयन कोण 30o में परिवर्तित हो जाता है। यदि हवाई जहाज़ 4500 मी. की ऊँचाई पर उड़ रहा है, तो हवाई जहाज़ की गति (मी./से. में) क्या है?
Options:
1) 50√3
2) 100√3
3) 200√3
4) 300√3
Correct Answer: 100√3
QID : 56 - एक पतंग आकाश में उड़ रही है। मैदान पर एक बिन्दु से पतंग तक धागे की लम्बाई 420 मी. है। मैदान से धागे का उन्नयन कोण 30o है। मान लीजिए की धागे में कोई ढीलापन नहीं है, तो पतंग की ऊँचाई (मीटर में) क्या है?
Options:
1) 210
2) 140√3
3) 210√3
4) 150
Correct Answer: 210
QID : 57 - एक गुब्बारा एक समान गति से बिन्दु P से छोड़ा जाता है। 6 मिनट पश्चात, बिन्दु P से 450√3 मीटर दूरी पर एक समीक्षक है जो देखता है कि गुब्बारे का उन्नयन कोण 60o है। मान लीजिए कि समीक्षा बिन्दु तथा बिन्दु P एक ही स्तर पर हैं। गुब्बारे की गति (मी,/से. में) क्या है?
Options:
1) 4.25
2) 3.75
3) 4.5
4) 3.45
Correct Answer: 3.75
QID : 58 -
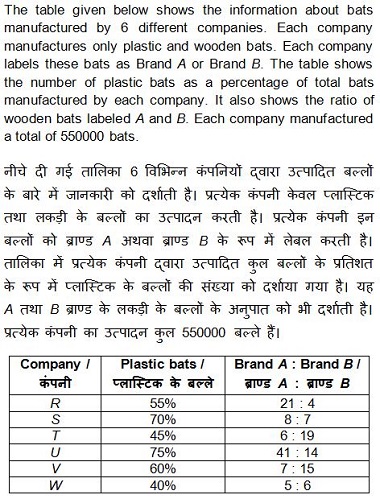
कंपनी T द्वारा उत्पादित ब्राण्ड A के लकड़ी के बल्लों की कुल संख्या क्या है?
Options:
1) 23420
2) 22990
3) 68920
4) 72600
Correct Answer: 72600
QID : 59 -

N = U द्वारा उत्पादित ब्राण्ड B के लकड़ी के बल्ले।
M = R तथा W द्वारा मिलकर उत्पादित कुल बल्ले।
N /M का मान क्या है?
Options:
1) 0.043
2) 0.061
3) 0.125
4) 0.087
Correct Answer: 0.061
QID : 60 -

P = S द्वारा उत्पादित ब्राण्ड B के लकड़ी के बल्लों तथा W द्वारा उत्पादित ब्राण्ड A के लकड़ी के बल्लों का योग।
Q = U द्वारा उत्पादित ब्राण्ड B के लकड़ी के बल्लों तथा ब्राण्ड A के लकड़ी के बल्लों का अंतर।
P – Q का मान क्या है?
Options:
1) 67500
2) 177700
3) 159500
4) 123500
Correct Answer: 159500
QID : 61 -

सभी 6 कंपनियों को मिलाकर, ब्राण्ड A के कितने लकड़ी के बल्लें बनाये गये हैं?
Options:
1) 691000
2) 724000
3) 683000
4) 716000
Correct Answer: 691000
QID : 62 -

X = V, U तथा T द्वारा उत्पादित प्लास्टिक के बल्लों का औसत।
Y = V द्वारा उत्पादित ब्राण्ड A के लकड़ी के बल्ले।
X – Y का मान क्या है?
Options:
1) 197600
2) 432890
3) 260000
4) 293300
Correct Answer: 260000
QID : 63 - एक ड्रम में 80 लीटर इथेनॉल है। इस तरल पदार्थ के 20 लीटर निकाल दिए जाते हैं और उसे पानी से प्रतिस्थापित किया जाता है। इस मिश्रण की 20 लीटर मात्रा को फिर से निकाला जाता है और पानी से प्रतिस्थापित किया जाता है। अब इस ड्रम में कितना पानी (लीटर में) मौजूद है?
Options:
1) 45
2) 40
3) 35
4) 44
Correct Answer: 35
QID : 64 - एक मिश्र धातु को 2000 रू / कि.ग्रा. लागत वाली धातु A और 400 रू / कि.ग्रा. लागत वाली धातु B को A : B = 3 : 1 अनुपात के मिश्रण से बनाया जाता है। इस मिश्र धातु के 8 कि.ग्रा. का मूल्य (रु में) क्या होगा?
Options:
1) 1600
2) 9800
3) 6400
4) 12800
Correct Answer: 12800
QID : 65 - A, B और C एक रेस्टोरेन्ट शुरू करने के लिए निवेश करते हैं। कुल निवेश 3 लाख रु था। B ने A की तुलना में 50,000 रु का अधिक निवेश किया और C ने B से 25,000 रु का कम निवेश किया। यदि साल के अंत में अर्जित लाभ 14,400 रु था, तो उस लाभ में C का हिस्सा क्या है (रु में)?
Options:
1) 3600
2) 4800
3) 6000
4) 7200
Correct Answer: 4800
QID : 66 - दो व्यापारियों A और B ने 5 : 8 के अनुपात में एक कारोबार में निवेश किया। उन्होंने व्यवसाय में कमाए गए लाभ के 30% धनराशि का पुनर्निवेश करने का निर्णय लिया। शेष लाभ को उन्होंने स्वयं के बीच वितरित कर लिया। अगर लाभ में A का शेयर 87,500 रुपये था, तो उस कारोबार में कितना लाभ (रूपये में) हुआ?
Options:
1) 227000
2) 250000
3) 375000
4) 325000
Correct Answer: 325000
QID : 67 - अकेले कार्य करते हुए A 27 घंटे में कार्य को पूरा कर सकता है और B इसे 54 घंटे में कर सकता है। C के शेयर का पता लगाएं (रु में) यदि A, B और C को 12 घंटे में एक कार्य पूरा करने के लिए 4,320 रु का भुगतान मिलता है, जिस पर उन्होंने एक साथ काम किया था।
Options:
1) 1440
2) 960
3) 1920
4) 1280
Correct Answer: 1440
QID : 68 - यदि A ने अकेले काम किया होता तो वह काम करने के लिए 63 घंटे लेता। B का हिस्सा क्या होगा, अगर A और B एक साथ काम करके उसे 36 घंटे में समाप्त करते हैं और इसके लिए 5,950 रुपये का भुगतान किया जाता है?
Options:
1) 3400
2) 3600
3) 2550
4) 2750
Correct Answer: 2550
QID : 69 - साथ में कार्य करते हुए A, B और C 12 दिनों में एक कार्य पूरा कर सकते हैं। यदि वे अकेले-अकेले काम करते हैं, तो A और B क्रमशः 55 दिनों और 66 दिनों में वह कार्य पूरा कर सकते हैं। यदि वह काम अकेले C करता है, तो उस काम को वह कितने दिनों में पूरा कर सकता है?
Options:
1) 22
2) 44
3) 20
4) 40
Correct Answer: 20
QID : 70 - B को एक कार्य पूरा करने के लिए A की तुलना में 10 घंटे अधिक समय लगता, अगर उनमें से प्रत्येक ने अकेले-अकेले काम किया होता। एक साथ कार्य करते हुए वे उस कार्य को 12 घंटे में पूरा कर सकते हैं। B को उस काम का 50% करने के लिए कितने घंटे लगेंगे?
Options:
1) 30
2) 15
3) 20
4) 10
Correct Answer: 15
QID : 71 - 20% का लगातार दो छूट देना ________ % के एक छूट देने के समान है।
Options:
1) 36
2) 40
3) 44
4) 50
Correct Answer: 36
QID : 72 - एक फुटकर विक्रेता अपने सामान का मूल्य 150% से बढ़ाकर अंकित करता है और 40% की छूट देता है। अगर वस्तु का मूल्य 800 रुपये है, तो उसका बिक्री मूल्य (रुपये में) क्या होगा?
Options:
1) 1200
2) 1500
3) 1000
4) 2000
Correct Answer: 1200
QID : 73 - ब्रांड A के एक टेलीवीजन पर 25% की छूट है और ब्रांड B के टेलीविज़न पर 40% की छूट है। छूट के बाद, B का मूल्य छूट के बाद, A के मूल्य से 2,250 रुपये अधिक है। A का अंकित मूल्य (रुपये में) क्या है, यदि B का अंकित मूल्य 35,000 रुपये है?
Options:
1) 18750
2) 21000
3) 25000
4) 17850
Correct Answer: 25000
QID : 74 - यदि अंकित मूल्य पर 60% छूट की पेशकश की जाती है और बिक्री मूल्य लागत मूल्य के बराबर हो जाती है, तो मूल्य कितने % से बढ़ाकर अंकित किया गया था?
Options:
1) 100
2) 250
3) 150
4) 40
Correct Answer: 150
QID : 75 - यदि 3 A = 6 B = 9 C; तो A : B : C क्या है?
Options:
1) 6 : 3 : 1
2) 6 : 3 : 2
3) 9 : 3 : 6
4) 9 : 3 : 1
Correct Answer: 6 : 3 : 2
QID : 76 - नौकरी के लिए कितने आवेदकों ने आवेदन किया था, यदि चयनित और गैर-चयनित आवेदकों के बीच का अनुपात 19:17 था। यदि 1,200 कम आवेदकों ने आवेदन किया होता और 800 आवेदक कम चुने जाते, तो चयनित और गैर-चयनित आवेदकों के बीच का अनुपात 1: 1 होता।
Options:
1) 6000
2) 7200
3) 8400
4) 4800
Correct Answer: 7200
QID : 77 - 10 और 20 के लिए तीसरा आनुपातिक क्या है?
Options:
1) 30
2) 25
3) 50
4) 40
Correct Answer: 40
QID : 78 - A और B के वेतन के योग और उनके वेतन के अंतर का अनुपात 11:1 है और B और C के वेतन के योग और उनके वेतन के अंतर का अनुपात भी 11:1 है। अगर A का वेतन सबसे ज्यादा है और C का वेतन सबसे कम है, तो B का वेतन (रु में) क्या है, दिया गया है कि उनका कुल वेतन 1,82,000 रु है?
Options:
1) 72000
2) 60000
3) 50000
4) 86400
Correct Answer: 60000
QID : 79 - यदि 8:11 के अनुपात में टिकट के मूल्य में वृद्धि की जाती है तो बेचे गये टिकटों की संख्या में 23:21 अनुपात से गिरावट आती है, तो राजस्व में हुई वृद्धि (रु में) क्या है, अगर टिकट की मूल्य में वृद्धि से पहले राजस्व 36,800 रु था?
Options:
1) 21250
2) 9400
3) 7850
4) 12850
Correct Answer: 9400
QID : 80 - पिता और मां की उम्र का अनुपात 11:10 था, जब उनके बेटे का जन्म हुआ था। पिता और मां की उम्र का अनुपात 19:18 होगा, जब पुत्र की आयु अपने वर्तमान आयु से दोगुनी हो जाएगी। पिता और मां के वर्तमान आयु का क्या अनुपात है?
Options:
1) 15 : 14
2) 14 : 13
3) 16 : 15
4) 17 : 16
Correct Answer: 15 : 14
QID : 81 - 3 संख्याओं में से, जिनका औसत 22 है, पहली संख्या दो अन्य संख्याओं के योग का 3/8-वां हिस्सा है। पहली संख्या क्या है?
Options:
1) 16
2) 20
3) 22
4) 18
Correct Answer: 18
QID : 82 - लगातार तीन विषम संख्याओं का औसत इनमें से सबसे बड़ी संख्या के 1/3 से 52 अधिक है। इनमें से सबसे छोटी संख्या क्या है?
Options:
1) 79
2) 75
3) 81
4) 77
Correct Answer: 77
QID : 83 - एक बल्लेबाज ने अपने करियर के 17-वें मैच में 98 रन बनायें। उसके प्रति मैच औसत रनों में 2.5 की वृद्धि हुई। 17-वें मैच से पहले उसका औसत क्या है?
Options:
1) 58
2) 60.5
3) 63
4) 55.5
Correct Answer: 55.5
QID : 84 - 100 और 200 के बीच के सभी संख्याओं का औसत क्या है, जो 13 से विभाज्य हो?
Options:
1) 147.5
2) 145.5
3) 143.5
4) 149.5
Correct Answer: 149.5
QID : 85 - एक विक्रेता 8 रु में 9 केले खरीदता है और 9 रु में 8 केले बेचता है। इसका लाभ या नुकसान (% में) क्या होगा?
Options:
1) 13.28% लाभ
2) 26.56% नुकसान
3) 26.56% लाभ
4) 13.28% नुकसान
Correct Answer: 26.56% लाभ
QID : 86 - यदि कोई स्टॉल 200 रु में पिज्जा बेचता है तो उसे 20% का नुकसान होता है, अगर वह 10% लाभ अर्जित करना चाहता है, तो उसे किस मूल्य में (रु में) बेचना चाहिए?
Options:
1) 250
2) 300
3) 275
4) 325
Correct Answer: 275
QID : 87 - एक थोक व्यापारी के पास 200 दर्जन आम थे। उसने इनमें से कुछ आमों को 20% लाभ पर और शेष आमों को 10% लाभ पर बेचा, ताकि वह सभी आमों को बेचने पर 13% लाभ कमा सके। उसने 20% लाभ पर कितने आम (दर्जनों में) बेचें?
Options:
1) 140
2) 60
3) 80
4) 120
Correct Answer: 60
QID : 88 - यदि बिक्री का मूल्य तीन गुना है और लागत मूल्य दाेगुना हो तो लाभ 65% हो जाएगा। मौजूदा लाभ (% में) क्या है?
Options:
1) 20
2) 15
3) 25
4) 10
Correct Answer: 10
QID : 1600 के 250% का 0.06% ____ के बराबर होगा।
Options:
1) 24
2) 0.24
3) 0.024
4) 2.4
Correct Answer: 2.4
QID : 90 - दो संख्याएं एक तीसरी संख्या से 90% और 75% कम है। पहली संख्या में कितने % में वृद्धि की जानी चाहिए ताकि वह दूसरी संख्या के बराबर हो जाए?
Options:
1) 250
2) 200
3) 150
4) 100
Correct Answer: 150
QID : 91 - जब किसी संख्या को 216 से बढ़ाया जाता है, तो यह स्वयं की 140% हो जाती है। वह संख्या क्या है?
Options:
1) 540
2) 756
3) 450
4) 675
Correct Answer: 540
QID : 92 - एक व्यक्ति अपनी संपत्ति का 30% भाग एक धर्मदाय संस्था को दान करता है। शेष राशि का क्रमशः 30% और 25% भाग अपनी पत्नी और बेटे को देता है। बाकी धनराशि वह अपनी तीन बेटियों के बीच समान रूप से विभाजित करता है। उसकी बेटियों में से एक को 42 लाख रू मिलते हैं। उस आदमी की कुल संपत्ति (लाख रु में) क्या थी?
Options:
1) 280
2) 400
3) 500
4) 350
Correct Answer: 400
QID : 93 - एक बस 20 घंटे में 720 कि.मी. की यात्रा तय करती है। मीटर / सेकंड में इसकी औसत गति की गणना करें।
Options:
1) 12
2) 15
3) 18
4) 10
Correct Answer: 10
QID : 94 - अगर एक नाव 21 किलोमीटर प्रति घंटे की गति से प्रवाह के विपरीत जाती है और 28 किलोमीटर प्रति घंटे की गति से उसी दूरी तक वापस आती है, तो कुल यात्रा की औसत गति (किलोमीटर / घंटा) क्या है?
Options:
1) 24.5
2) 24
3) 25
4) 25.4
Correct Answer: 24
QID : 95 - दो धावकों A और B ने 12 कि.मी. / घंटा और 16 कि.मी. / घंटा की गति से एक-दूसरे की तरफ दौड़ना शुरु किया। वे एक घंटे और 30 मिनट के बाद आपस में मिलें। प्रारंभ करते समय वे एक दूसरे से कितनी दूर (कि.मी. में) थे?
Options:
1) 42
2) 36
3) 40
4) 45
Correct Answer: 42
QID : 96 - उड़ान A को आमतौर पर 7200 किलोमीटर की दूरी तय करने के लिए उड़ान B से 1 घंटा अधिक लगता है। इंजन में खराबी आने की वजह से उड़ान B की गति 1/6 के एक कारक से नीचे गिर जाती है, इसलिए उसी यात्रा को पूरी करने के लिए उड़ान B को उड़ान A की तुलना में 36 मिनट अधिक लगते हैं। उड़ान A (किलोमीटर / घंटा) की गति क्या है?
Options:
1) 800
2) 900
3) 750
4) 720
Correct Answer: 800
QID : 97 - सालाना चक्रवृद्धि से गणना करते हुए 10% प्रति वर्ष वार्षिक चक्रवृद्धि ब्याज की दर से 2,000 रू से कितने वर्षों में 662 रुपए मिलेंगे?
Options:
1) 3
2) 2
3) 4
4) 5
Correct Answer: 3
QID : 98 - तिमाही आधार पर 1 वर्ष में प्रति वर्ष 40% की दर से 80,000 रूपयों पर अर्जित चक्रवृद्धि ब्याज क्या होगा?
Options:
1) 28317
2) 37128
3) 18732
4) 21387
Correct Answer: 37128
QID : 99 - एक निवेशक ने शेयर बाजार में अपनी बचत का निवेश किया। उसके निवेश के मूल्य में क्रमशः पहले वर्ष में 12% और दूसरे वर्ष में 9% वृद्धि हुई। यदि दो साल के बाद उसके निवेश का मूल्य 97,664 रु हो गया, तो उसने कितना निवेश (रू में) किया था?
Options:
1) 81000
2) 75000
3) 80000
4) 72000
Correct Answer: 80000
QID : 100 - ब्याज दर (% में) क्या है, यदि एक निश्चित राशि पर 3 साल के लिए अर्जित साधारण ब्याज 6,000 रु और 2 साल के लिए अर्जित चक्रवृद्धि ब्याज 4,160 रु है?
Options:
1) 9
2) 8
3) 12
4) 6
Correct Answer: 8




