(Guidance Programme) Combined Higher Secondary Level [CHSL] (10+2) Exam : Basic Algebra
Basic Algebra
Basic Algebra
A Civil Servant should be well-versed in basics of Algebra. In the Civil
Services Aptitude Test Paper 2, in Basic Numeracy, certainly there will be asked
some questions based on equations and their roots.
Polynomials
Polynomial
An expression in term of some variable(s) is called a polynomial.
For example
f(x) = 2x – 5 is a polynomial in variable x
g(y) = 5y2 – 3y + 4 is a polynomial in variable y
Note that the expressions like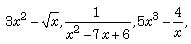 etc.
are not polynomials. Thus, a rational x integral function of ‘x’ is said to be a
polynomial, if the powers of ‘x’ in the terms of the polynomial are neither
fractions nor negative. Thus, an expression of the form
etc.
are not polynomials. Thus, a rational x integral function of ‘x’ is said to be a
polynomial, if the powers of ‘x’ in the terms of the polynomial are neither
fractions nor negative. Thus, an expression of the form
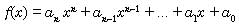 is called a polynomial in variable x where n be a positive integer and a0, al,
...,an be constants (real numbers).
is called a polynomial in variable x where n be a positive integer and a0, al,
...,an be constants (real numbers).
Degree of a Polynomial
The exponent of the highest degree term in a polynomial is known as its degree.
For example

Linear Polynomial
A polynomial of degree one is called a linear polynomials. In general f(x) = ax + b, where a ¹ 0 is a linear polynomial.
For example
f(x) = 3x – 7 is a binomial as it contains two terms.
g(y) = 8y is a monomial as it contains only one terms.
Quadratic Polynomials
A polynomial of degree two is called a quadratic polynomials. In general f(x) = ax2 + bx + c, where a ¹ 0 is a quadratic polynomial.
For example
f(x) = x2 – 7x + 8 is a trinomial as it contains 3 terms
g(y) = 5x2 – 2x is a binomial as it contains 2 terms
p(u) = 9x2 is a monomial as it contains only 1 term
Cubic Polynomial
A polynomial of degree 3 is called a cubic polynomial in general.
f(x) = ax3 + bx3 + cx + d, a ¹ 0 is a cubic polynomial.
For example
f(x) = 2x3 – x2 + 8x + 4
Biquadratic Polynomial
A fourth degree polynomial is called a biquadratic polynomial in general.
f(x) = ax4 + bx3 + cx2 + dx + e, a ¹ 0 is a bi quadratic polynomial.
Zero of a Polynomial
A real number a is a zero (or root) of a polynomial f(x), if f (a) = 0
For example If x = 1 is a root of the polynomial 3x3 – 2x2 + x – 2, then
f(l)= 0
f(x) = 3x3 – 2x2 + x – 2, f(1) = 3 × 13 – 2 × 12 + 1 – 2 = 3 – 2 + 1 – 2 = 0, As
f(1) = 0 x = 1 is a root of polynomial f(x)
(1) A polynomial of degree n has n roots.
(2) A linear polynomial of f(x) = ax + b, a ¹ 0 has a unique root given by x =
(3) Every real number is a root of the zero polynomial.
(4) A non-zero constant polynomial has no root.
Remainder Theorem
Let f(x) be a polynomial of a degree greater than or equal to one and a be any real number, if f(x) is divisible by (x – a), then the remainder is equal to f(a) .
Example 1: Find the remainder when f(x) = 2x3 – 13x2 + 17x + 10 is divided by
x – 2.
Solution. When f(x)is divided by x – 2, then remainder is given by
f(2) = 2(2)3 – 13(2)2 + 17(2) + 10 = 16 – 52 + 34 + 10 = 8
Thus, on dividing f(x) = 22 – 13x2 + 17x + 10 by x – 2, we get the remainder 8.
© SSCPORTAL.IN

