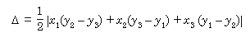Study Material for SSC CGL, CHSL, MTS, Prasar Bharti, FCI Exams : Coordinate Geometry
Coordinate Geometry
Coordinate Geometry is also called Analytical Geometry. It is that branch of geometry in which we use two numbers called coordinates to indicate the position of a point in a plane.
Cartesian Coordinate System
The horizontal line x´ is called the x-axis and the vertical
line y´ oy is called the y-axis and together they are called the coordinate
axes. The point of intersection of these two axes is called the origin. Let P be
any point in a plane. From P draw perpendiculars to the coordinate axes meeting
the x-axis in M and y-axis in N. Here, OM(x) is the x-coordinate or absicssa of
a point P. Similarly, ON(y) is the y-coordinate or ordinate of point P.
This position of the point P in the plane with respect to the coordinate axes
is represented by the ordered pair (x, y) and this system is called the
cartesian coordinate system.
The coordinates of the origin O are (0, 0). Also, x´ox and y´oy divide the plane
into four regions called quadrants.
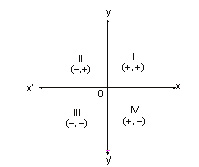
1. xoy is quadrant I. Here, x-coordinate is positive and y-coordinate is positive. (+,+)
2. x´oy is quadrant II. Here, x-coordinate is negative and y-coordinate is positive. (–, +)
3. x´oy is quadrant III. Here, x-coordinate is negative and y-coordinate is negative. (–, –)
4. xoy´ is quadrant IV. Here, x-coordinate is positive and y-coordinate is negative. (+, –)
eg,
(1,5) lies in first quadrant
(–2,3) lies in second quadrant
(–2, –4) lies in third quadrant
(4,–2) lies in fourth quadrant
The coordinate of origin is (0, 0).
The ordinate of every point on x-axis is 0.
The ordinate of every point on y-axis is 0.
Distance between Two Points: Let P (xl, yl) and Q (x2,y2) be any two points on the plane, then the distance between P and Q is represented as PQ is given by
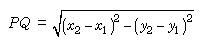
The distance of the point P(x, y) from the origin (0, 0) is
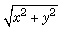
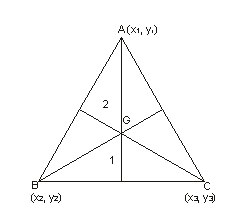
Centroid If A(xl, yl), B(x2, y2) and C(x3, y3) are the vertices of a triangle,
then the three medians of the triangle intersect at its centroid and the
centroid divides the median in the ratio 2 : 1. A
Coordinates of the point G are given by
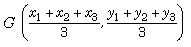
Area of a Triangle: If A(xl, yl), B(x2 , y2) and C(x3, y3 ) be three vertices of
a triangle ABC, then its area is given by