Basic Algebra

A Civil Servant should be well-versed in basics of Algebra. In the Civil Services Aptitude Test Paper 2, in Basic Numeracy, certainly there will be asked some questions based on equations and their roots.
Polynomials
Polynomial
An expression in term of some variable(s) is called a polynomial.
For example
f(x) = 2x – 5 is a polynomial in variable x
g(y) = 5y2 – 3y + 4 is a polynomial in variable y

Note that the expressions like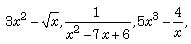etc. are not polynomials. Thus, a rational x integral function of ‘x’ is said to be a polynomial, if the powers of ‘x’ in the terms of the polynomial are neither fractions nor negative. Thus, an expression of the form
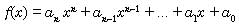is called a polynomial in variable x where n be a positive integer and a0, al, ...,an be constants (real numbers).

Degree of a Polynomial

The exponent of the highest degree term in a polynomial is known as its degree.

Linear Polynomial

A polynomial of degree one is called a linear polynomials. In general f(x) = ax + b, where a ¹ 0 is a linear polynomial.

Quadratic Polynomials

A polynomial of degree two is called a quadratic polynomials. In general f(x) = ax2 + bx + c, where a ¹ 0 is a quadratic polynomial.

Cubic Polynomial

A polynomial of degree 3 is called a cubic polynomial in general.

f(x) = ax3 + bx3 + cx + d, a ¹ 0 is a cubic polynomial.

Biquadratic Polynomial

A fourth degree polynomial is called a biquadratic polynomial in general.

f(x) = ax4 + bx3 + cx2 + dx + e, a ¹ 0 is a bi quadratic polynomial.

Zero of a Polynomial

A real number a is a zero (or root) of a polynomial f(x), if f (a) = 0

Remainder Theorem

Let f(x) be a polynomial of a degree greater than or equal to one and a be any real number, if f(x) is divisible by (x – a), then the remainder is equal to f(a) .

Factor Theorem

Let f(x) be a polynomial of degree greater than or equal to one and a be any real number such that f(a) = 0, then (x – a) is a factor of f(x).
Conversely, if (x – a) is a factor of f(x), then f(a) = 0.

Useful Formulae

(i) (x + y)2 = x2 + y2 + 2xy
(ii) (x – y)2 = x2 + y2 – 2xy
(iii) (x2 – y2) = (x + y) (x – y)
(iv) (x + y)3 = x3 + y3 + 3xy(x + y)
(v) (x – y)3 = x3 – y3 – 3xy(x – y)
(vi) (x3 + y3) = (x + y) (x2 + y2 – xy)
(vii) (x3 – y3) = (x – y) (x2 + y2 + xy)
(viii) (x + y + z)2 = x2 + y2 + z2 + 2(xy + yz + zx)
(ix) (x3 + y3 + z3 – 3xyz) = (x + y + z) (x2 + y2 + z2 – xy – yz – zx)
(x) If x + y + z = 0, then x3 + y3 + z3 = 3xyz